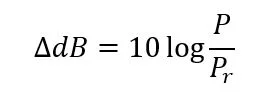Amplifiers 101, power and volume
/In summary:
If you couldn't watch the video, here's what you missed.
There's a lot of mystique in music
A common misconception is how loud a small amp can get
I annoyed the neighbors by blasting two different guitar amps at full volume in a small apartment
References:
Molberg's Law: If it sounds good, it is good!
NIOSH 98-126: Occupational noise exposure
This blog adds extra info (read: numbers) that fellow tech nerds might find interesting but aren't required reading.
Let's talk decibels.
Your ears don't hear in a linear fashion, our closest approximation is decibels. I'll give a full breakdown on dBs in a future post but for now, here's the fundamental tool for our discussion:
Pr - A reference power
P - Your subject's power
Head 2 head
Our two test amps for the guitar portion:
Fender Frontman 10g
- Solid state
- 10W
- 6" 4ohm speaker
- 109.5 dBA max
Marshall DSL40c
- Tube
- 40W RMS
- 12" 16ohm speaker
- 116.2 dBA max
Using our equation and using the Fender as our reference we get
10log(40/10)=6.02dB
Our actual difference is 6.7 dB according to my simple cell phone test for a 11.3% error in our quick experiment. What's going on?
Control group
What stays the same in these two tests?
The signal - The same person used the same guitar at the same settings to play the same chord through the same cable. The two amps were both at full volume and set to comparable gain.
The environment - both tests took place in the same room with minimal shifting.
The measuring tools - I used a nifty SPL (sound pressure level) meter on my phone. The phone's mic was roughly the same distance from the amp both times and oriented the same way for each test. I wouldn't dream of saying that SPL meter is calibrated accurately but I was measuring the difference rather than the actual values. I'll double check this later.
Peak & RMS
We'll start with the obvious, notice in the specs the Marshall lists RMS power. RMS is essentially an average, it's lower than the peak power. For sine waves
Wrms = 0.707 * Wpeak
But guitars don't put out sine waves. For distorted sounds like I used in the video you get something closer to a square wave. In ideal square waves peak and RMS are identical but due to factors such as slew rate, Q factor, saturation and a few other concepts that will be covered in other articles there will be some difference between peak and RMS in real amplifiers. Since the Fender doesn't specify what kind of power it's using I'll assume peak for argument. The numbers also could have been rounded for aesthetics. The 10 could be anywhere between 7-13W without me calling foul.
For a minute we'll assume all other factors are equal
6.7=10log(40/Pf)
10^(0.67) = 40/Pf
Pf = 40/4.68
Pf = 8.55 Wrms
Conceivably, the 10g could be as low as 8.6 Wrms, but there's more to consider here.
Second opinion
You'll notice in the video I had a Rhode M5 condensor sitting in front of each amp before playing them. This was actually a secondary measurement. The gain on the mic is identical in each case and the distance from the amp is 1' straight from the center cone in both instances. The M5 is directional so room noise is less of a factor in this case as well. Looking at the peak output for these we have
10g -16.7dBFS
40c -5.5dBFS
So now the carefully controlled group gives us a difference of 11.2dB! Good grief what happened??
Sensitivity, frequency response & weighting
The 40c and 10g both use very different speakers. For the Marshall we are lucky enough to know what the speaker is: the Celestion seventy 80 and it lists an important stat: a sensitivity of 98dB. Sensitivity is a measure of how much noise comes out of a speaker at a given power, usually 1W, at a given distance, usually 1m. Celestion is vague on how it measures sensitivity but by their rating a 40 watt amp should produce:
10log(40) + 98 = 114dB SPL
We can call this our calibration correction (I am trying to keep some semblance of scientific rigor here) so the Fender now has a calibrated volume of 107.3dBA SPL on the phone and 102.8dB SPL on the M5. Different speakers can have drastically different sensitivities. A 4dB difference in sensitivity is not out of the question but 2dB is common within a brand, much less across them.
Before leaving the topic of sensitivity, we have to also account for what type of signal Celestion used for their test. It could be white noise, pink noise, or a single frequency tone. I used an Emaj chord on a modified C/SH-1. This matters because of the frequency response. The 6" Fender speaker is far less responsive to low frequency noise than the Celestion and far more responsive to high frequency noise. It's possible that my test tone was simply out of the Fender's comfort zone.
I used my cell phone to try accounting for the extra low end the Celestion delivered through weighting. Low frequency noise produces a drastically lower SPL when A-weighted when compared to the M5. In fact since the M5 is a cardioid pattern low frequencies are enhanced and count for more than an unweighted scale.